
Other mirrors types for"grazing schemes"- look
here
,
for a example
toroidal mirrors
or
ellipsoidal mirrors
Off-axis parabolic (also often written OAP - from Off Axis Parabolic) mirrors are part of the surface of a paraboloid rotation (see figure below, red shows the reflecting surface of the mirror, yellow - radiation, orange shows the optical axis of the parabaloid, violet - angle of incidence of radiation (AOI)).
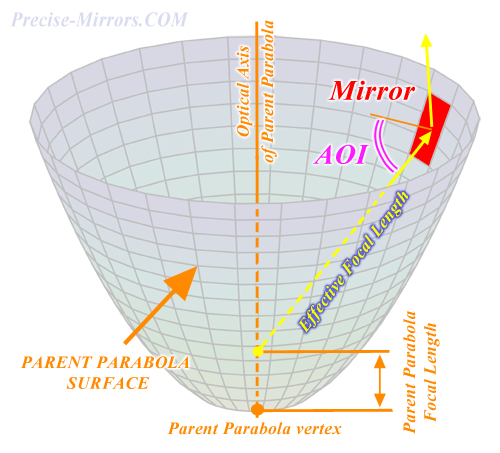
The main property of a paraboloid: the ray emerging from its focus after reflection from its surface will move parallel to the optical axis of the paraboloid. Thus, OAP mirrors make it possible to obtain a collimated beam from a point source that is NOT located on the optical axis of the reflecting mirror itself (whereas for an axial parabola the source is always located on the optical axis of the parabola). OAP operation scheme is not axisymmetric (whereas the axial parabola has an axisymmetric scheme).
The usual standard operating scheme for OAP mirrors implies an angle of incidence AOI of no more than 90 degrees (and for precise OAP mirrors the angle of incidence AOI will be several times smaller, see the left side of the figure below). However, if we increase the angle of incidence AOI to 70-89 degrees (see the right side of the figure below), it turns out that the beam seems to "slides over the mirror", "graze the mirror", which is why operation at such large angles of incidence is called a "grazing schemes" (and the angle is 90 degrees minus the angle of incidence is called the "grazing angle").
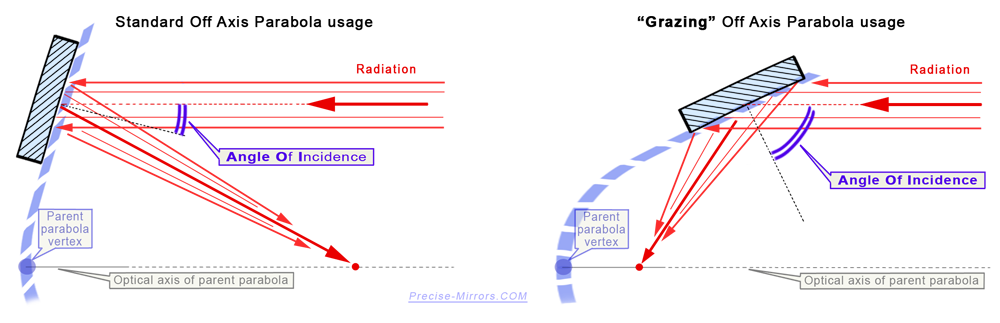
Such large angles of incidence make it possible to use such off-axis parabolic mirrors to reflect radiation with short wavelengths (less than 50-100 nm and up to a few nm), since in order to achieve a noticeable coefficient in this spectral range To reflect a mirror, it is necessary to use very large angles of incidence (usually 70-85 degrees and up to 89 degrees).
In fact, when using "grazing schemes", there are only two tasks for which off-axis parabolic mirrors are used. The first task is the work of one mirror, which either focuses a collimated beam to a point, or, on the contrary, creates a collimated beam of radiation diverging from a point source (see the left side of the figure below). The second task is the work of two conjugated mirrors, with the help of which a collimated beam is first created from a point and then it will focus back to the point (see the right side of the picture below).
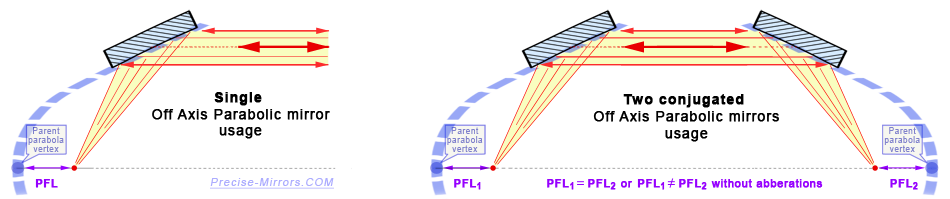
Important! Most often, conjugate toroidal mirrors are usually used to solve the second task. However, they do this not because that this approach gives a good result, but because almost no one in the world knows how to make accurate off-axis parabolic mirrors for "grazing schemes". Moreover, there is a widespread misconception that using two identical conjugates toroidal mirrors allows You to get rid of large spherical distortions (in theory this is true - the second toroid should compensate for the distortions introduced by the first toroid). But in real practice everything is much more complicated, for example, see the third page of our standard quotation , where the stability of a real optical setup with two identical conjugate toroidal mirrors is simulated). Also, you should remember that for off-axis parabolic surfaces it is possible to match different mirrors (thereby obtaining a reduced or enlarged source image). If the conjugate toroidal mirrors are different - then appear large spherical abberations and this distortion will be even with ideal precision in the manufacture of reflective surfaces). As a result - focused spot (image of a source) turns into a “shapeless mess” with millimeter size).
| Mirror minimal and maximal sizes: | from 40 mm to 1200 mm | |
| Mirror substrate material: | Astrositall, by request: Zerodur, UV FS, Si and other. | |
| Coatings: | Metallic (Ag, Au, Al) and special EUV|XUV. | |
| Manufacture accuracy (RMS, λ=633 nm) | Base | Maximal |
| surface shapes, spherical mirrors | up to λ/140 | up to λ/400 |
| surface shapes, aspherical mirrors | up to λ/100 | up to λ/300 |
| Radiuses manufacture accuracy | up to ±0.05% | up to ±0.001% |
| Surface microroughness, RMS | 0.3 nm | 0.15 нм |
| Cosmetic quality (per square inch) | 40/20 scratch/dig | 10/5 scratch/dig |
The main advantage of off-axis parabolic mirrors is that they have no aberrations at all (at least from a practical point of view). Thus, with fairly good accuracy in manufacturing the shape of the reflective surface, it does not matter at all what the distance to the source and before the image, no matter what the angle of incidence and what size of the mirror - the result of OAP mirror work will always be close to the ideally possible.
In fact, the only disadvantage of off-axis parabolic mirrors is the high complexity of their production and, as a consequence, their high cost and longer production times (especially for mirrors with large asphericity). Moreover, according to as of the spring of 2024, we have no data that anyone else in the world besides us can manufacture such off-axis parabolic mirrors, in which, at an angle of incidence AOI of more than 70 degrees (the off-axis angle is more than 140 degrees), the accuracy of the surface shape at the working angle will be better than λ/4 RMS (where λ=633 nm). At the same time, simple arithmetic indicates that for operation in the spectral range less than 50-100 nm it's necessary to have shape accuracy in the worst case λ/50-λ/100 (where λ=633 nm). That is why, for this second task, the world usually uses two identical toroidal mirrors (although this approach gives noticeably worse results). To use ellipsoidal mirrors it doesn't make sense for a task like this.
Typically, it is very important for the customer how small a spot in the image plane can be formed by the mirror (see figure below). Even if the task is to obtain a collimated beam from a point source of radiation, the value of the minimum focused spot size allows You to evaluate the quality (for example, divergence) of the resulting collimated beam.
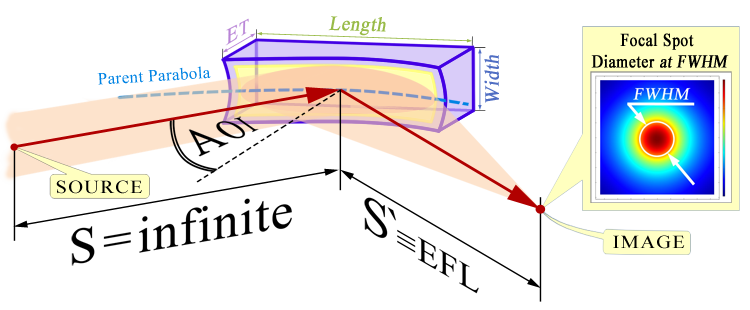
The size of the spot in the image plane depends on many different factors, but from real practice for ellipsoidal mirrors this is only the accuracy of manufacturing the shape of the mirror surface and sometimes diffraction limitations at the operating wavelength. Also, the accuracy of the adjustment is often extremely important, since sometimes, for example, the error in the position of the mirror is only a few microns can increase the diameter of the focused spot several times.
The general principle is that the closer the size of focused spot
to the diffraction limit, the more expensive such a mirror is.
It depends on Your task and the funds allocated for the purchase. The most competent and correct way would be to fill out our special "request form" (here it is help in filling out (pdf) ). It is also advisable to attach to the request form a description of Your optical design (at least in words), in which the mirror will operate and all this send to our email quote@precise-mirrors.ru. Next, our specialists will select several suitable options for You (see example of a typical quote for single mirror or for two conjugated mirrors ).
You can also send a detailed exact specification of the mirror You need with drawings, a description of the type of surface shape, calculated radii, with all tolerances, etc. But even in this case, it is better to add at least minimal information on the angle of incidence, the size of the source and the desired image size. From our extensive practice, in such cases it is often possible to at least optimize the radius, with which the result will be slightly better and the customer does not incur any additional costs.
You also don’t have to fill out "request form" , and do not send a detailed exact specification of the mirror you need, but instead send a description of Your task (mirror) in any form to the same email address quote@precise-mirrors.ru. But in this case, such a request may take much longer to process.